[자료구조/Data Structure] 파이썬으로 이진 탐색 트리(Binary Search Tree) 자료구조 알아보기

트리 구조란?

노드와 브랜치를 이용해서 사이클을 이루지 않도록 구성한 데이터 구조,

그 모습이 마치 나무 같아서 트리(Tree)라고 부른다.

 

트리의 용어

• Node : 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 Node에 대한 Branch 정보 포함)
• Root Node : 트리 맨 위에 있는 노드
• Level : root node를 level 0으로 하였을 때, 하위 branch로 연결되 노드의 깊이를 나타냄
• Parent Node : 어떤 node의 이전 레벨에 연결된 node
• Child Node : 어떤 node의 다음 레벨에 연결된 node
• Leaf Node : child node가 하나도 없는 node
• Sibling : 동일한 Parent Node를 가진 node
• Depth : 트리에서 node가 가질 수 있는 최대 level

 

트리의 용어를 설명한 그림

위와 같이 그림을 보면 트리는 노드와 브랜치로 이루어져 있는 자료구조다.

최상위 노드는 루트 노드 불리며 루트 노드 밑으로 쭉 연결 되어있다.

 

여기서 이진 트리 개념을 추가하면 이진탐색트리(Binary Search Tree)가 되는데

이진탐색트리의 노드는 항상 최대 두개의 노드만 가지며 

그 노드의 왼쪽 자식 노드는 항상 부모 노드보다 값이 작고

오른쪽 자식 노드는 항상 부모 노드보다 값이 크다.

또한 모든 노드의 키 값은 중복되지 않는다.

 

위 그림을 보면 루트 노드는 31의 값을 가지고 있고 루트 노드의 왼쪽 자식 노드의 값은 16으로 31보다 작고,

반대로 루트 노드의 오른쪽 자식 노드의 값은 37로 31보다 크다.

 

위와 같은 규칙이 루트 노드의 왼쪽 자식 노드인 16에게도 마찬가지로 적용된다.

16의 왼쪽 자식 노드 값은 16보다 작고 오른쪽 자식 노드 값은 16보다 크다.

이와 같이 이진탐색트리는 모든 노드가 이런 규칙을 가지고 있다.

 

이진탐색트리 구현하기

그럼 이제 본격적으로 파이썬을 통해 이진탐색트리를 구현해보자.

 

우선, 노드를 어떻게 구현할까?

노드는 양쪽으로 자식을 가질 수 있다.

물론 자식을 하나도 안 가질 수도 있다.

 

따라서 노드에게 왼쪽 및 오른쪽을 가리킬 수 있는 포인터 변수를 선언해주면 될 것이다.

 

그걸 그림으로 그려보면 이런 식일 거다.

노드 그림

위 그림과 같이 노드가 생겼다고 생각하면 된다.

왼쪽과 오른쪽이 다음 자식 노드를 가리키는 포인터 변수를 가지고 있고,

중간에 실제 데이터를 가지고 있는 구조다.

 

따라서 이것을 코드로 작성하면 이런식으로 작성할 수 있다.

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

 

이제는 이 노드를 활용하는 실질적인 이진탐색트리를 만들 차례다.

 

우선 이진탐색트리 클래스가 있다고 가정하고,

이진탐색트리 클래스를 객체로 만들 때 루트 노드의 값을 초기값으로 받을 수도 있고, 

안 받을 수도 있는데 필자는 초기화시 루트 노드의 값을 받지 않는 방식으로 구현했다.

bst = Binary_Search_Tree() # 초기값을 받지 않는다.
bst = Binary_Search_Tree(32) # 초기값을 받는다.

 

이런 식으로 초기값을 받지 않는다고 가정 했을 때 이진탐색트리의 생성자는 아래와 같이 작성할 수 있다.

class Binary_Search_Tree:
    def __init__(self):
        self.root = None

위와 같이 생성자를 작성하면 root는 값을 가리키고 있지 않는다.

 

insert 함수 구현

이제는 이진탐색트리의 노드를 삽입하는 함수를 구현해볼 것이다.

 

구현하기 전에 어떻게 이진탐색트리의 삽입을 구현할 수 있을까?

대충 생각해보면 노드들을 순회 하면서 현재 노드가 삽입 할려는 노드보다 크면 왼쪽으로 이동하고,

현재 노드가 삽입 할려는 노드보다 작으면 오른쪽으로 이동하면 될 것 같다.

 

일단 코드를 먼저 보자.

def insert(self, data):
    if self.root is None:
        self.root = Node(data)
    else:
        self.base = self.root
        while True:
            if data == self.base.data:
                print("중복된 KEY 값")
                break
            elif data > self.base.data:
                if self.base.right is None:
                    self.base.right = Node(data)
                    break
                else:
                    self.base = self.base.right
            else:
                if self.base.left is None:
                    self.base.left = Node(data)
                    break
                else:
                    self.base = self.base.left

코드를 위에서 아래 순으로 설명하자면 

 

if self.root is None:
	self.root = Node(data)

이 부분은 root가 가리키는 값이 없을 때 동작하는 구간이다.

root가 가리키는 값이 없다는 것은 해당 트리에 노드가 한개도 없다는 것이다.

따라서 이 코드는 처음으로 들어오는 데이터를 루트로 만들어 주는 역할을 한다.

 

그리고 이 다음 줄의 코드인 else 구문부터 본격적인 삽입 로직이 구현되어 있다.

else:
  self.base = self.root
  while True:
      if data == self.base.data:
          print("중복된 KEY 값")
          break

base 변수는 root부터 시작하여 트리를 순회하면서 삽입할 데이터의 적절한 위치를 찾아주는 역할을 한다.

while 구문안에 트리를 쭉 순회할 로직을 구현해 줄 것이고, 이진탐색트리의 데이터 값은 중복을 허용하지 않는다고 했으니

위의 if문과 같이 들어온 데이터가 이미 트리에 있는 데이터면 데이터가 중복됨을 알리고 break를 통해 while문을 빠져나가는 예외 처리를 

해줬다.

elif data > self.base.data:
    if self.base.right is None:
        self.base.right = Node(data)
        break
    else:
        self.base = self.base.right
else:
    if self.base.left is None:
        self.base.left = Node(data)
        break
    else:
        self.base = self.base.left

위 코드는 데이터의 삽입 위치를 찾는 코드다.

삽입할 데이터가 현재 노드보다 크면 현재 노드의 right가 가르키는 노드가 있는지

확인하고 만약 가르키는 노드가 없다면 데이터가 삽입될 위치가 된다. 

따라서 위와 같이 self.base.right에 노드를 삽입하고 break문을 통해 빠져나간다.

하지만 right가 가르키는 노드가 있다면 이미 공간을 차지하고 있는 것이므로

base를 현재 base보다 큰 값이 base.right로 재할당 해준다.

 

만약 삽입할 데이터가 현재 노드보다 작은 경우에는 위의 로직을 반대로만 구현하면 된다.

이렇게 이진탐색트리의 삽입 함수를 만들 수 있다.

 

search 함수 구현

다음으로 구현할 함수는 search 함수다.

파라미터로 받은 데이터 값이 트리안에 있으면 True를 리턴하고 없으면 False를 리턴한다.

 

우선 코드를 보자.

def search(self, data):
    self.base = self.root
    while self.base:
        if self.base.data == data:
            return True
        elif self.base.data > data:
            self.base = self.base.left
        else:
            self.base = self.base.right
    return False

먼저 구현한 함수인 insert와 비슷한 방법이다.

root부터 base로 지정해주고 while문으로 노드들을 순회하면서 찾으면 True를 리턴하고,

찾을 데이터가 현재 노드의 데이터 보다 작다면(여기서는 elif문) 노드를 왼쪽으로 이동시키고,

찾을 데이터가 현재 노드의 데이터 보다 크다면(else문) 노드를 오른쪽으로 이동시킨다.

그러면 자연스럽게 노드들을 순회하면서 데이터를 찾을 수 있다.

 

remove 함수 구현

다음으로 구현할 함수는 노드를 삭제하는 remove함수다.

이진탐색트리를 구현하면서 제일 난이도가 높고 조건이 까다로운 함수가 이 remove 함수라고 생각한다.

 

우선 코드를 보자면 이렇다.

def remove(self, data):
    self.searched = False
    self.cur_node = self.root
    self.parent = self.root
    while self.cur_node:
        if self.cur_node.data == data:
            self.searched = True
            break
        elif self.cur_node.data > data:
            self.parent = self.cur_node
            self.cur_node = self.cur_node.left
        else:
            self.parent = self.cur_node
            self.cur_node = self.cur_node.right
    if self.searched:
        # root를 지우는 경우
        if self.cur_node.data == self.parent.data:
            self.root = None
        else:
            # [CASE 1] 삭제하는 node가 leaf node인 경우
            if self.cur_node.left is None and self.cur_node.right is None:
                if self.parent.data > self.cur_node.data:
                    self.parent.left = None
                else:
                    self.parent.right = None

            # [CASE 2] 삭제하는 node의 자식이 하나인 경우
            elif self.cur_node.left is not None and self.cur_node.right is None:
                if self.parent.data > data:
                    self.parent.left = self.cur_node.left
                else:
                    self.parent.right = self.cur_node.left
            elif self.cur_node.left is None and self.cur_node.right is not None:
                if self.parent.data > data:
                    self.parent.left = self.cur_node.right
                else:
                    self.parent.right = self.cur_node.right

            # [CASE 3] 삭제하는 node의 자식이 둘인 경우
            elif self.cur_node.left is not None and self.cur_node.right is not None:
                self.tmp_parent = self.cur_node.right
                self.tmp_cur = self.cur_node.right
                while self.tmp_cur.left:
                    self.tmp_parent = self.tmp_cur
                    self.tmp_cur = self.tmp_cur.left
                if self.tmp_cur.right is not None:
                    self.tmp_parent.left = self.tmp_cur.right
                else:
                    self.tmp_parent.left = None
                if self.parent.data > data:
                    self.parent.left = self.tmp_cur
                else:
                    self.parent.right = self.tmp_cur
                self.tmp_cur.left = self.cur_node.left
                self.tmp_cur.right = self.cur_node.right
    else:
        print("존재하지 않는 데이터")

상당히 길다..

한번에 이해하기는 어려우니 부분적으로 설명하자면 

 

우선 remove 함수를 구현할 때 먼저 삭제하려는 데이터가 트리안에 존재하는지 체크해야 된다.

그 부분이 아래 코드에 해당한다.

def remove(self, data):
    self.searched = False
    self.cur_node = self.root
    self.parent = self.root
    while self.cur_node:
        if self.cur_node.data == data:
            self.searched = True
            break
        elif self.cur_node.data > data:
            self.parent = self.cur_node
            self.cur_node = self.cur_node.left
        else:
            self.parent = self.cur_node
            self.cur_node = self.cur_node.right

이 코드는 삭제하려는 데이터가 트리에 있으면 searched를 True로 바꿔주고 없으면 False를 유지한다.

찾는 과정 중에 cur_node가 찾는 데이터의 노드로 할당 되고 cur_node에 부모 노드가 parent로 할당 된다.

 

그림으로 보자면

위와 같이 만약 remove(41)을 하게 된다면, searched는 True로 할당되고, cur_node는 41 데이터를 가지고 있는 노드로 할당되고 parent는 41의 부모 노드인 39 데이터를 가진 노드로 할당 된다.

 

이렇게 해당 데이터를 찾게 되고 cur_node와 parent가 할당되면 본격적으로 노드를 삭제할 준비는 됐다.

삭제할 준비가 되면 삭제되는 경우의 수를 생각해야 되는데 그 경우의 수는 아래와 같다.

 

1. 삭제되는 노드가 리프 노드인 경우 (삭제되는 노드가 자식 노드가 없는 경우)

 

2. 삭제되는 노드의 자식이 하나인 경우

 

3. 삭제되는 노드의 자식이 둘인 경우

 

이제 경우의 수를 알았으니 차근차근 하나씩 구현하면 된다.

 

먼저 리프 노드를 삭제하는 경우(1번)를 알아보겠다.

사실 이 경우가 삭제하는 로직 중에서 제일 쉽다.

 

만약 cur_node의 left와 right가 None(null) 이라면 그 노드는 리프노드이고 

cur_node.data가 parent.data보다 크면 parent의 right를 None으로 바꿔주고,

cur_node.data가 parent.data보다 작으면 parent의 left를 None으로 바꿔주면 된다.

 

이것을 코드로 작성하면 아래와 같다.

# [CASE 1] 삭제하는 node가 leaf node인 경우
if self.cur_node.left is None and self.cur_node.right is None:
    if self.parent.data > self.cur_node.data:
        self.parent.left = None
    else:
        self.parent.right = None

 

다음은 삭제하는 노드의 자식이 하나인 경우(2번)를 알아보겠다.

이것도 조금만 생각해보면 그렇게 어렵지는 않게 해결할 수 있다.

 

그림을 다시 보자면

여기서 39를 삭제하는 경우인데..

39를 지워주고 37의 right를 41로 연결해주면 된다.

만약에 41밑에 자식이 몇개가 있더라도 단순히 41을 37의 오른쪽 자식으로

연결하면 이진탐색트리에 규칙을 절대 위반하지 않는다.(자식 노드가 오른쪽이던지 왼쪽이던지 상관없다)

직접 그림을 그려서 확인해보기 바란다.

 

자, 그러면 이것을 코드로 구현하려면 어떻게 해야될까?

우선 자식이 한개인 경우는 다시 두가지로 나눌 수 있다.

 

1. 삭제하는 노드에 자식이 왼쪽만 있는 경우

2. 삭제하는 노드에 자식이 오른쪽만 있는 경우

 

그걸 코드로 작성하면 이렇다.

# [CASE 2] 삭제하는 node의 자식이 하나인 경우
elif self.cur_node.left is not None and self.cur_node.right is None:
	삭제로직...
elif self.cur_node.left is None and self.cur_node.right is not None:
	삭제로직...

 

그리고 이 안에 삭제 로직을 구현하면 아래와 같다.

# [CASE 2] 삭제하는 node의 자식이 하나인 경우
elif self.cur_node.left is not None and self.cur_node.right is None:
    if self.parent.data > data:
        self.parent.left = self.cur_node.left
    else:
        self.parent.right = self.cur_node.left
elif self.cur_node.left is None and self.cur_node.right is not None:
    if self.parent.data > data:
        self.parent.left = self.cur_node.right
    else:
        self.parent.right = self.cur_node.right

삭제하는 노드(cur_node)에 자식이 왼쪽에만 있는 경우 (위에서는 첫번째 elif 구문)

만약에 cur_node의 data(여기서는 cur_node.data가 아니라 그냥 data라고 적었는데 파라미터로 data를 받고 그 데이터가 있는지 이미 위 로직에서 파악했기 때문에 이렇게 적어도 무방하다)가 parent보다 작다면 cur_node는 parent의 left랑 연결 되어 있다는 뜻이고,

cur_node에 left자식만 있는 것을 위에서 이미 확인했기 때문에 

self.parent.left = self.cur_node.left 이런식으로 할당해서 마무리 할 수 있다.

반대에 경우에도 마찬가지로 left, right만 잘 구분해서 구현하면 된다.

 

다음으로는 

remove의 마지막 삭제 로직인 

삭제하는 노드의 자식이 둘인 경우(3번)를 알아보겠다.

이게 제일 머리 아프다..

 

우선 기준을 잡을 필요가 있다.

37은 자식 노드가 두개이고,

37을 삭제하게 되면 그 자리에 공백이 생기게 되고 

적절한 노드를 찾아서 그 공백을 채워야 된다.

 

적절한 노드를 어떻게 찾을까?

조금 생각을 해볼 필요가 있는데, 이진탐색트리는 임의에 노드를 기준으로 그 노드의 오른쪽 자식은 항상

그 노드보다 크고 왼쪽 자식은 항상 그 노드보다 작다.

 

이런 점을 이용하면 

37의 오른쪽 자식, 즉 39에서 

가장 작은 노드로 37에 공백을 채워주면 될 것 같다.

(이것을 반대로 해도 된다. 37의 왼쪽 자식 중 제일 큰 값으로 37에 공백을 채워줘도 된다.)

 

자 위에 방법을 코드로 구현하려면 삭제하는 노드 (여기서는 37)에

오른쪽 자식 중 제일 작은 값을 가르키는 임시 변수가 있어야 될 것 같다.

또 그것에 부모 노드를 가르키는 변수도 필요하다.

 

그것을 구하는 과정은 이렇다.

elif self.cur_node.left is not None and self.cur_node.right is not None:
    self.tmp_parent = self.cur_node.right
    self.tmp_cur = self.cur_node.right
    while self.tmp_cur.left:
        self.tmp_parent = self.tmp_cur
        self.tmp_cur = self.tmp_cur.left

천천히 생각해보면 이해할 수 있다!

일단 elif 구문은 삭제하는 노드에 자식이 두개인 경우를 뜻하고 

임시로 만든 변수 tmp_parent와 tmp_cur가 삭제하는 노드의 오른쪽 자식 노드부터 시작하여 계속

left로 향하며 제일 작은 값이 될때 까지 이동한다.

 

그렇게 해서 while 구문을 빠져나가면 자연스럽게 tmp_cur는 삭제하는 노드의 오른쪽 자식 중 제일

작은 값을 가르키고 있을 것이다.

if self.tmp_cur.right is not None:
    self.tmp_parent.left = self.tmp_cur.right
else:
    self.tmp_parent.left = None
if self.parent.data > data:
    self.parent.left = self.tmp_cur
else:
    self.parent.right = self.tmp_cur
self.tmp_cur.left = self.cur_node.left
self.tmp_cur.right = self.cur_node.right

그 후 코드는 이렇다.

일단 첫 if 구문은 tmp_cur의 right가 존재하면 동작하는 구문이다.

 

아래 그림을 보자

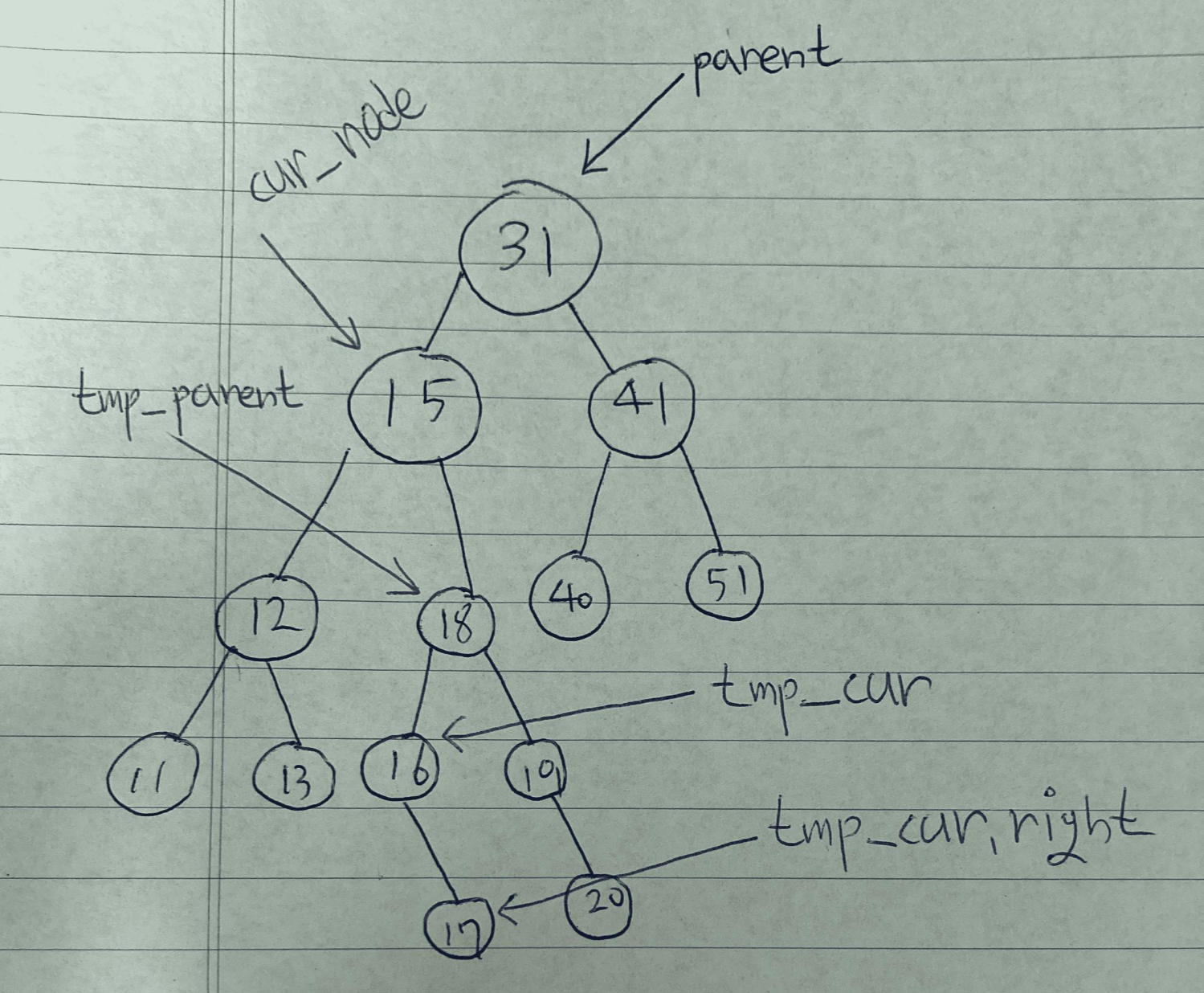
위 그림은 tmp_cur의 right가 존재하는 트리를 그린 그림이다.

만약에 이렇게 존재한다면 tmp_parent에 left가 tmp_cur의 right 즉 17을 가르키게 되고

아니면 그냥 None을 가르키면 된다. 

 

그리고 다음 구문인 아래 코드부터는

if self.parent.data > data:
    self.parent.left = self.tmp_cur
else:
    self.parent.right = self.tmp_cur

삭제하는 데이터가 parent보다 크면 parent에 right에

parent보다 작으면 parent에 left에 tmp_cur을 연결해준다.

 

여기서는 15를 삭제한다고 가정하면 15가 31보다 작으니 15 자리에 16이 위치하게 된다.

 

그 후에 

self.tmp_cur.left = self.cur_node.left
self.tmp_cur.right = self.cur_node.right

16에 left에 15에 left값(12)을,

16에 right에 15에 right값(18)을 할당해주면 15에 위치에 16이 자리잡게 된다..

 

이렇게 삭제하는 노드의 자식이 둘인 경우를 구현할 수 있다..

 

트리의 순회

이제는 트리의 순회를 구현해볼 차례다.

트리에 데이터가 잘 들어가있다고 해도 확인이 안 되면 소용이 없을 것이다.

그래서 트리를 순회하면서 데이터를 확인하는 로직을 구현할 것인데

크게 세가지 방법이 있다.

 

1. 전위 순회 (pre-order traverse) : Root -> 왼쪽 -> 오른쪽

2. 중위 순회 (in-order traverse) : 왼쪽 -> Root -> 오른쪽

3. 후외 순회 (post-order traverse) : 왼쪽 -> 오른쪽 -> Root

 

일단 코드를 보면 이렇다.

# 전위 순회
def pre_order_traverse(self, node):
    if not node:
        return
    print(node.data, end=' ')
    self.pre_order_traverse(node.left)
    self.pre_order_traverse(node.right)


# 중위 순회
def in_order_traverse(self, node):
    if not node:
        return
    self.in_order_traverse(node.left)
    print(node.data, end=' ')
    self.in_order_traverse(node.right)


# 후위 순회
def post_order_traverse(self, node):
    if not node:
        return
    self.post_order_traverse(node.left)
    self.post_order_traverse(node.right)
    print(node.data, end=' ')

기본적으로 재귀함수를 통해 구현하고 순회하는 순서에 따라 전위, 중위, 후위로 나뉜다.

 

2021.06.06 - [Algorithm] - [알고리즘/Algorithm] 파이썬으로 재귀함수 알아보기

[알고리즘/Algorithm] 파이썬으로 재귀함수 알아보기

재귀함수를 알면 쉽게 이해할 수 있을 것이다. 

전위는 Root -> 왼쪽 -> 오른쪽

중위는 왼쪽 -> Root -> 오른쪽

후위는 왼쪽 -> 오른쪽 -> Root

순으로 순회 하면서 데이터를 출력한다.

 

remove 함수에 삭제하는 노드의 자식이 둘인 경우(3번)을 구현하면서 예시를 든 트리를 전 -> 중 -> 후 순서로 순회를 하면 이런 결과를 얻을 수 있다.

b = Binary_Search_Tree()
b.insert(31)
b.insert(15)
b.insert(41)
b.insert(12)
b.insert(18)
b.insert(40)
b.insert(51)
b.insert(11)
b.insert(13)
b.insert(16)
b.insert(19)
b.insert(17)
b.insert(20)

b.pre_order_traverse(b.root)
print()
b.in_order_traverse(b.root)
print()
b.post_order_traverse(b.root)

```
31 15 12 11 13 18 16 17 19 20 41 40 51 
11 12 13 15 16 17 18 19 20 31 40 41 51 
11 13 12 17 16 20 19 18 15 40 51 41 31 
```

 

마치며

자료구조를 공부하며 자료구조를 보는 눈이 살짝은? 높아진 것 같다..

확실히 알고 쓰는거랑 모르고 쓰는거랑 하늘과 땅차이가 있는 것 같고

구현하는 과정이 재밌어서 만족스러웠다.

 

파이썬으로 구현한 이진탐색트리 전체 코드

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None


class Binary_Search_Tree:
    def __init__(self):
        self.root = None

    def insert(self, data):
        if self.root is None:
            self.root = Node(data)
        else:
            self.base = self.root
            while True:
                if data == self.base.data:
                    print("중복된 KEY 값")
                    break
                elif data > self.base.data:
                    if self.base.right is None:
                        self.base.right = Node(data)
                        break
                    else:
                        self.base = self.base.right
                else:
                    if self.base.left is None:
                        self.base.left = Node(data)
                        break
                    else:
                        self.base = self.base.left

    def search(self, data):
        self.base = self.root
        while self.base:
            if self.base.data == data:
                return True
            elif self.base.data > data:
                self.base = self.base.left
            else:
                self.base = self.base.right
        return False

    def remove(self, data):
        self.searched = False
        self.cur_node = self.root
        self.parent = self.root
        while self.cur_node:
            if self.cur_node.data == data:
                self.searched = True
                break
            elif self.cur_node.data > data:
                self.parent = self.cur_node
                self.cur_node = self.cur_node.left
            else:
                self.parent = self.cur_node
                self.cur_node = self.cur_node.right
        if self.searched:
            # root를 지우는 경우
            if self.cur_node.data == self.parent.data:
                self.root = None
            else:
                # [CASE 1] 삭제하는 node가 leaf node인 경우
                if self.cur_node.left is None and self.cur_node.right is None:
                    if self.parent.data > self.cur_node.data:
                        self.parent.left = None
                    else:
                        self.parent.right = None

                # [CASE 2] 삭제하는 node의 자식이 하나인 경우
                elif self.cur_node.left is not None and self.cur_node.right is None:
                    if self.parent.data > data:
                        self.parent.left = self.cur_node.left
                    else:
                        self.parent.right = self.cur_node.left
                elif self.cur_node.left is None and self.cur_node.right is not None:
                    if self.parent.data > data:
                        self.parent.left = self.cur_node.right
                    else:
                        self.parent.right = self.cur_node.right

                # [CASE 3] 삭제하는 node의 자식이 둘인 경우
                elif self.cur_node.left is not None and self.cur_node.right is not None:
                    self.tmp_parent = self.cur_node.right
                    self.tmp_cur = self.cur_node.right
                    while self.tmp_cur.left:
                        self.tmp_parent = self.tmp_cur
                        self.tmp_cur = self.tmp_cur.left
                    if self.tmp_cur.right is not None:
                        self.tmp_parent.left = self.tmp_cur.right
                    else:
                        self.tmp_parent.left = None
                    if self.parent.data > data:
                        self.parent.left = self.tmp_cur
                    else:
                        self.parent.right = self.tmp_cur
                    self.tmp_cur.left = self.cur_node.left
                    self.tmp_cur.right = self.cur_node.right
        else:
            print("존재하지 않는 데이터")

    # 전위 순회
    def pre_order_traverse(self, node):
        if not node:
            return
        print(node.data, end=' ')
        self.pre_order_traverse(node.left)
        self.pre_order_traverse(node.right)

    # 중위 순회
    def in_order_traverse(self, node):
        if not node:
            return
        self.in_order_traverse(node.left)
        print(node.data, end=' ')
        self.in_order_traverse(node.right)

    # 후위 순회
    def post_order_traverse(self, node):
        if not node:
            return
        self.post_order_traverse(node.left)
        self.post_order_traverse(node.right)
        print(node.data, end=' ')

 

 

참고자료

• 이진탐색트리 시각화 제공 웹 : https://visualgo.net/bn/bst